Programování v C# prakticky - 2.díl - Rozhodovací struktury

24. 6. 2012 Milan Suk C# 3 komentáře 1453

V tomto díle seriálu programování v C# prakticky si napíšeme aplikace na procvičení rozhodovacích struktur. U aplikací se budu opÄ›t držet matematického zaměření. První aplikace bude na výpočet koÅ™enů kvadratické rovnice, pÅ™ičemž budeme kontrolovat kolik Å™ešení má a druhá bude na výpočet hodnoty funkce tangens a budeme pÅ™itom hlídat, jestli uživatel nezadal hodnotu 90°, pro kterých není tato funkce definovaná

Kvadratická rovnice

Začneme jemnou teorií, aby se zájemci o programování z nižších ročníků základních škol nestráceli.

Kvadratická rovnice je taková rovnice, která obsahuje promÄ›nnou povýšenou na exponent 2 (x²). Obecný zápis této rovnice je potom ax² + bx + c = 0. Pro výpočet se používat tzv. diskriminant. Ten má vzorec D = b² - 4ac. Potom na základÄ› toho, jakou hodnotu má diskriminant se zjišÅ¥uje, kolik bude mít rovnice Å™ešení. 

• Pokud D = 0, potom má rovnice jedno dvojnásobné Å™ešení (protože kvadratická rovnice musí mít buď dvÄ›, nebo žádné Å™ešení),
• Pokud D > 0, má rovnice dvÄ› Å™ešení,
• Pokud D < 0, nemá rovnice v množinÄ› R žádné Å™ešení (v množinÄ› komplexních čísel ano, ale to nyní nebudeme uvažovat)

Řešení rovnice získáme pomocí následující ho vztahu :

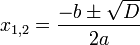
Setavení algorytmu

Po uživateli budeme potÅ™ebovat pouze koeficienty a, b a c, pÅ™ičemž koeficient a nesmí být roven nule, jinak by byl kvadratické člen roven nule a nejednalo by se již o kvadratickou rovnici, ale o rovnici lineární. Další samozÅ™ejmostí je, že v textových polích musí nÄ›co být napsaného, takže string zadaný pro koeficienty b a c nesmí být null.

Pokud budou tyto podmínky splnÄ›ny pÅ™ejdeme k samotnému výpočetu diskriminantu. To nebude, vhledem k tomu, že se v nÄ›m nachází pou mocnina druhého stupnÄ› a tu můžeme vyjádÅ™it jakou součin, žádný problém. 

V posledním kroku musíme zjistit, jstli se hodnota promÄ›nné, do které jsme uložili výsledek diskriminantu, rovná nula, je vÄ›tší než nula a nebo jestli je menší než nula. Na základÄ› toho potom vypočítáme hodnotu. (pozn.) V pÅ™ípadÄ› jednoho koÅ™enu si samozÅ™ejmÄ› výraz upravíme na - b / 2a, protože pokud se hodnota diskriminantu rovná nule, potom i jeho odmocnina je samozÅ™ejmÄ› nula, proto ho není tÅ™eba uvažovat.

Musíme si ještÄ› uvÄ›domit, že hodnoty, s kterými budeme pracovat budou s velkou pravdÄ›podobností desetinná, proto využijeme datového typu Double (popÅ™. float apod.). Na základÄ› tÄ›chto poznatků můžeme snadno sestavit odpovídající zdrojový kód :

// Počítáme s tím, že textová pole mají označení textBox1, textBox2 a textBox3
if (string.IsNullOrEmpty(textBox1.Text) || string.IsNullOrEmpty(textBox2.Text) 
    || string.IsNullOrEmpty(textBox3.Text) || textBox1.text == 0) // Kontrola vstupu od uživatele
{
 MessageBox.Show("ChybnÄ› zadané potÅ™ebné údaje", "Chyba", MessageBoxButtons.OK, MessageBoxIcon.Warning); // vypsat chybovou hlášku
}
else
{
 double a = Convert.ToDouble(textBox1.Text); // Koeficient a
 double b = Convert.ToDouble(textBox2.Text); // Koeficient b
 double c = Convert.ToDouble(textBox3.Text); // Koeficient c
  
 double diskriminant = b * b - (4 * a * c); 
 if (diskriminant == 0) // jedno Å™ešení
 {
  double x = -b / 2 * a;
  MessageBox.Show("Rovnice má jeden reálný koÅ™en : x = " + x + ".", "Výsledek");
 }
 else if (diskriminant > 0) // dvÄ› různá Å™ešení
 {
  double x1 = (-b - Math.Sqrt(diskriminant)) / 2 * a;
  double x2 = (-b + Math.Sqrt(diskriminant)) / 2 * a;
  MessageBox.Show("Rovnice má dva reálné koÅ™eny : x1 = " + x1 + "; x2 = " + x2 + ".", "Výsledek");
 }
 else if (diskriminant < 0) // žádné reálné Å™ešení
 {
  MessageBox.Show("Rovnice nemá žádný reálný koÅ™en !", "Výsledek");
 }
}

Výsledná fungující aplikace vipadá asi jako na obrázku níže.

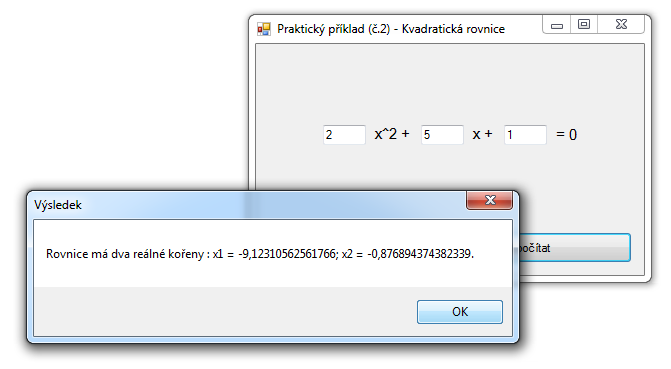
Výpočet funkce tangens

Další pÅ™íklad bude velice jednoduchý. Vypočteme hodnotu funkce tangens a budeme muset hlídat pouze to, jestli je hodnota různá od 90°. Funkce tangens totiž není pro tuto hodnotu definovaná. Proč lze docela pÄ›knÄ› vidÄ›t z obrázku níže. Protože funkční hodnota pro cos(90°) = 0, tak by se tato nula objevila ve jmenovateli zlomku, což samozÅ™ejmÄ› nelze. 

V našem algorytmu nejdÅ™íve zjistíme, jestli je hodnota získaná od uživatele rovna nula, nebo jestli je null a pokud ne vypočítáme hodnotu funkce tangens a vypíšeme ji do komponenty Label. Pro samotný výpočet můžeme použít buď pÅ™mo funkci tangens a nebo vzorec nahoÅ™e. Goniometrické funkce jsou k nalezení ve tÅ™ídÄ› Math (Math.Sin, Math.Cos, Math.Tan), ovšem pozor tyto funkce neočekávají úhel ve stupních, nýbrž v radiánech, proto musíme ještÄ› Å™ed použití funkce pÅ™evést vstup uživatele na radiány.

if (string.IsNullOrEmpty(textBox1.Text) || Convert.ToDouble(textBox1.Text) == 90) // Je prázdný nebo hodnoty 90
{
 MessageBox.Show("Byl zadán chybný vstup", "Chyba", MessageBoxButtons.OK, MessageBoxIcon.Warning); // Vypsat chybovou hlášku
}
else
{
 double x = Convert.ToDouble(textBox1.Text) / (180 / Math.PI); // Uložit do promÄ›nné x a rovnou pÅ™evést radiány
 double vysledek = Math.Sin(x) / Math.Cos(x); // Dopočítání hodnoty funkce tangens
 label.Text = "y = " + vysledek; // Zapsání výsledku
}

Výslednou aplikace můžete vidÄ›t na obrázku níže.

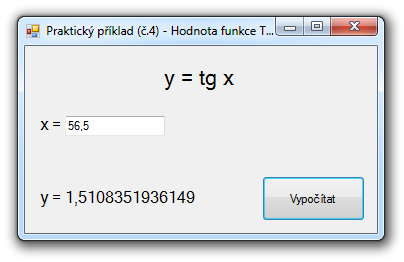
ZávÄ›r

To je k tomuto dílu opÄ›t vše. V dalším dílu budeme pokračovat aplikacemi na procvičení cyklů. Můžete se tÄ›šit napÅ™. na aplikace jako tÅ™eba výpočet pÅ™esné hodnoty faktoriálu.